不经意伪随机函数(Oblivious Pseudorandom Functions,简称 OPRF),是一种在密码学协议和隐私保护技术中广泛使用的基本原语。哈佛大学、波茨坦大学、IBM 欧洲研究院和哈索普拉特纳研究所合著的论文《SoK: Oblivious Pseudorandom Functions》基于数学证明和分析来比较不同类型的 OPRF 在安全性、效率、功能性等方面的优劣,全面概述如何利用 OPRF 来改善互联网用户的隐私,进一步展示了 OPRF 的理论和实践能力。
预备知识
- OPRF 的定义和安全性模型: OPRF 是一种两方协议,其中一方(发送方)持有一个伪随机函数(PRF)的密钥k,另一方(接收方)持有一个输入x。协议的目标是让接收方得到PRF在k和x上的输出f(k,x),而发送方不得到任何信息。 OPRF 的安全性要求满足正确性、单向性、隐私性和可验证性等属性。
- OPRF 的基本构建模块: OPRF 的构造依赖于一些密码学原语,如伪随机函数、双线性映射、同态加密等。伪随机函数是一种可以用密钥和输入生成随机输出的函数,具有不可区分性和抗碰撞性等特点。双线性映射是一种可以在两个群之间进行映射的函数,具有可计算性和非退化性等特点。同态加密是一种可以在密文上进行运算的加密方式,具有可加性或可乘性等特点。
- OPRF 的相关概念: OPRF 除了基本的定义和安全性模型外,还有一些扩展或变体的概念,如单向性、可验证性、可扩展性等。单向性是指接收方不能从f(k,x)中反推出x或k的信息。可验证性是指接收方能够验证f(k,x)是否正确。可扩展性是指接收方能够从f(k,x)中派生出其他相关的值,如f(k,x+1)或f(k,g(x))等。
OPRF 的分类
- OPRF 的分类标准: OPRF 可以根据它们使用的底层PRF的类型分为四大类,分别是 Naor-Reingold型、Dodis-Yampolskiy 型、Hashed Diffie-Hellman 型和通用型。这四类 OPRF 有不同的效率、安全性和功能特点。
- Naor-Reingold 型 OPRF :这类 OPRF 基于 Naor-Reingold PRF,它是一种基于双线性映射的 PRF,可以实现单向性和可验证性。这类 OPRF 的优点是效率高,缺点是需要大量的公共参数和存储空间。
- Dodis-Yampolskiy 型 OPRF :这类 OPRF 基于 Dodis-Yampolskiy PRF,它是一种基于哈希函数和同态加密的PRF,可以实现单向性和可扩展性。这类 OPRF 的优点是不需要公共参数和存储空间,缺点是效率低。
- Hashed Diffie-Hellman 型 OPRF :这类 OPRF 基于 Hashed Diffie-Hellman PRF,它是一种基于哈希函数和 Diffie-Hellman 协议的PRF,可以实现单向性和可扩展性。这类 OPRF 的优点是效率高且安全性强,缺点是需要双线性映射或椭圆曲线群。
- 通用型 OPRF :这类 OPRF 基于任意的 PRF,它使用一种通用的构造方法将任意的PRF转化为一个 OPRF 。这类 OPRF 的优点是适用范围广,缺点是效率低且安全性弱。
OPRF 的属性
- OPRF 的属性概述: OPRF 除了基本的单向性和隐私性外,还有一些其他的属性,如可验证性、可扩展性、可重用性、可组合性等。这些属性可以影响 OPRF 的效率、安全性和功能。
- OPRF 的可验证性:可验证性是指接收方能够验证f(k,x)是否正确。这个属性可以防止发送方作弊或错误地计算f(k,x)。可验证性可以通过使用零知识证明、签名或双线性映射等技术来实现。
- OPRF 的可扩展性:可扩展性是指接收方能够从f(k,x)中派生出其他相关的值,如f(k,x+1)或f(k,g(x))等。这个属性可以增加 OPRF 的功能和灵活性。可扩展性可以通过使用同态加密、哈希函数或双线性映射等技术来实现。
- OPRF 的可重用性:可重用性是指发送方能够使用同一个密钥k来与多个接收方进行 OPRF 协议。这个属性可以减少发送方的计算和存储开销。可重用性可以通过使用哈希函数或双线性映射等技术来实现。
- OPRF 的可组合性:可组合性是指多个 OPRF 协议能够安全地组合在一起,不影响各自的安全性和功能。这个属性可以增加 OPRF 的应用范围和复杂度。可组合性可以通过使用通用组合定理或混合模型等技术来实现。
OPRF 在密码学原语中的位置
- OPRF 与其他密码学原语的关系: OPRF 与其他密码学原语有着密切的联系,可以看作是一种特殊的安全多方计算、一种特殊的盲签名、一种特殊的可验证加密或一种特殊的随机预言机等。
- OPRF 作为其他密码学原语的构建模块: OPRF 可以用来构建其他密码学原语,如可验证加密、零知识证明、私有信息检索、私有集合运算等。这些原语可以利用 OPRF 的单向性、可验证性和可扩展性等属性来提高效率和安全性。
- OPRF 作为其他密码学原语的变体或扩展: OPRF 也可以从其他密码学原语中派生出不同的变体或扩展,如可重用 OPRF 、可组合 OPRF 、多方 OPRF 、分布式 OPRF 等。这些变体或扩展可以增加 OPRF 的功能和灵活性。
OPRF 在隐私保护技术中的应用
- OPRF 在隐私保护技术中的作用: OPRF 可以用来实现一些隐私保护技术,如密码认证、密码存储、密码恢复、密码搜索、密码交换等。这些技术可以利用 OPRF 的单向性、可验证性和可扩展性等属性来保护用户的密码和数据。
- OPRF 在密码认证中的应用: OPRF 可以用来实现一种安全的密码认证协议,如 OPAQUE。这种协议可以让用户使用自己选择的密码来登录一个远程服务器,而不需要将密码或其哈希值泄露给服务器或其他攻击者。这种协议可以防止字典攻击、中间人攻击和离线攻击等。
- OPRF 在密码存储中的应用: OPRF 可以用来实现一种安全的密码存储方案,如V OPRF 。这种方案可以让用户将自己的密码或其他敏感数据存储在一个云服务商处,而不需要将明文或其哈希值泄露给云服务商或其他攻击者。这种方案可以防止数据泄露、数据篡改和数据丢失等。
- OPRF 在密码恢复中的应用: OPRF 可以用来实现一种安全的密码恢复机制,如 BlindSeer。这种机制可以让用户在忘记自己的密码时,通过一个可信任的第三方来恢复自己的密码或其他敏感数据,而不需要将明文或其哈希值泄露给第三方或其他攻击者。这种机制可以防止第三方滥用、第三方妥协和第三方不可用等。
- OPRF 在密码搜索中的应用: OPRF 可以用来实现一种安全的密码搜索技术,如 BlindBox。这种技术可以让用户在一个加密的数据库中进行关键字搜索,而不需要将关键字或其哈希值泄露给数据库提供者或其他攻击者。这种技术可以防止数据库提供者窥探、数据库提供者篡改和数据库提供者拒绝服务等。
- OPRF 在密码交换中的应用: OPRF 可以用来实现一种安全的密码交换协议,如 Private Set Intersection (PSI)。这种协议可以让两个用户交换他们各自持有的一组元素(如联系人、喜好、历史记录等),而不需要将元素或其哈希值泄露给对方或其他攻击者。这种协议可以防止信息泄露、信息伪造和信息篡改等。



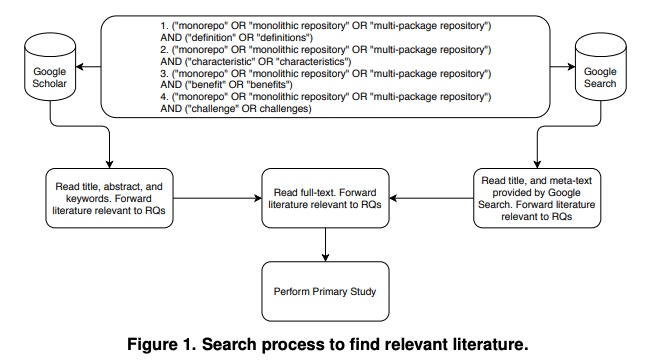 一分钟读论文:《Monorepo:多声体文献综述》
一分钟读论文:《Monorepo:多声体文献综述》